Aligning Model Properties via Conformal Risk Control
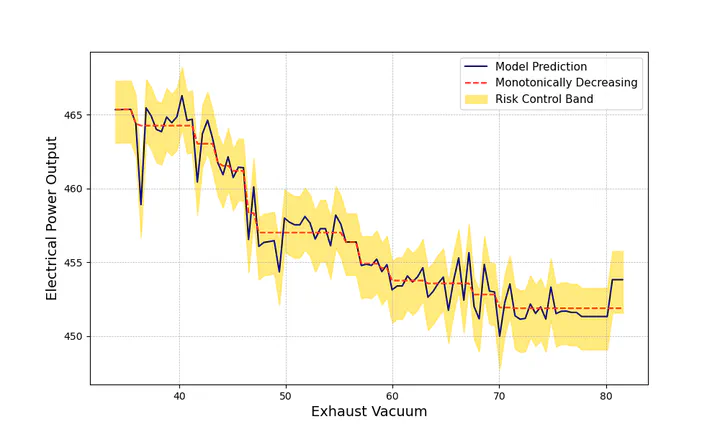 Univariate Partial Dependence plot highlighting the main theorem, which shows that we can find a function satisfying the desired property of monotonicity within the conformal band.
Univariate Partial Dependence plot highlighting the main theorem, which shows that we can find a function satisfying the desired property of monotonicity within the conformal band.Abstract
AI model alignment is crucial due to inadvertent biases in training data and the underspecified machine learning pipeline, where models with excellent test metrics may not meet end-user requirements. While post-training alignment via human feedback shows promise, these methods are often limited to generative AI settings where humans can interpret and provide feedback on model outputs. In traditional non-generative settings with numerical or categorical outputs, detecting misalignment through single-sample outputs remains challenging, and enforcing alignment during training requires repeating costly training processes. In this paper we consider an alternative strategy. We propose interpreting model alignment through property testing, defining an aligned model f as one belonging to a subset P of functions that exhibit specific desired behaviors. We focus on post-processing a pre-trained model f to better align with P using conformal risk control. Specifically, we develop a general procedure for converting queries for testing a given property P to a collection of loss functions suitable for use in a conformal risk control algorithm. We prove a probabilistic guarantee that the resulting conformal interval around f contains a function approximately satisfying P. We exhibit applications of our methodology on a collection of supervised learning datasets for (shape-constrained) properties such as monotonicity and concavity. The general procedure is flexible and can be applied to a wide range of desired properties. Finally, we prove that pre-trained models will always require alignment techniques even as model sizes or training data increase, as long as the training data contains even small biases.
Type
Publication
Short version appeared in NeurIPS 2024